2022-06-27

112. Path Sum

Description

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1:

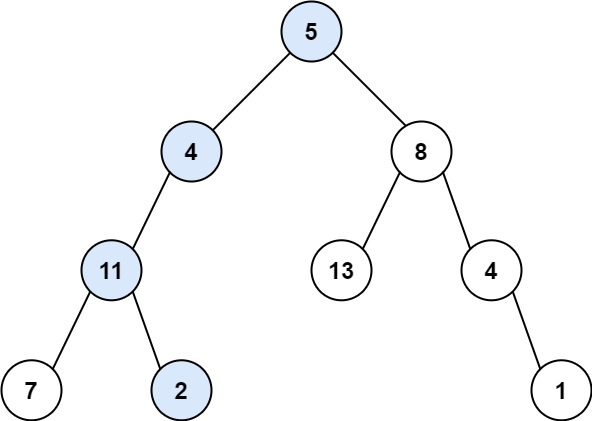
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
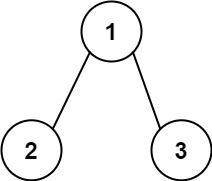
Explanation: The root-to-leaf path with the target sum is shown.

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false
Explanation: There two root-to-leaf paths in the tree:
(1 --> 2): The sum is 3.
(1 --> 3): The sum is 4.
There is no root-to-leaf path with sum = 5.

Example 3:

Input: root = [], targetSum = 0
Output: false
Explanation: Since the tree is empty, there are no root-to-leaf paths.

Constraints:

• The number of nodes in the tree is in the range [0, 5000].

• -1000 <= Node.val <= 1000

• -1000 <= targetSum <= 1000

Solution

Approach #0: DFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func hasPathSum(root *TreeNode, targetSum int) bool {
    if root == nil {
        return false
    }
    if root.Left == nil && root.Right == nil {
        return root.Val == targetSum
    }
    return hasPathSum(root.Left, targetSum-root.Val) || hasPathSum(root.Right, targetSum-root.Val)
}

Approach #1: BFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func hasPathSum(root *TreeNode, targetSum int) bool {
    if root == nil {
        return false
    }
    nodeQ := []*TreeNode{root}
    valQ := []int{0}
    for len(nodeQ) > 0 {
        node := nodeQ[0]
        nodeQ = nodeQ[1:]
        val := valQ[0]
        valQ = valQ[1:]
        if node.Left == nil && node.Right == nil && val+node.Val == targetSum {
            return true
        }
        if node.Left != nil {
            nodeQ = append(nodeQ, node.Left)
            valQ = append(valQ, node.Val+val)
        }
        if node.Right != nil {
            nodeQ = append(nodeQ, node.Right)
            valQ = append(valQ, node.Val+val)
        }
    }
    return false
}