2022-06-03

117. Populating Next Right Pointers in Each Node II

Description

Given a binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

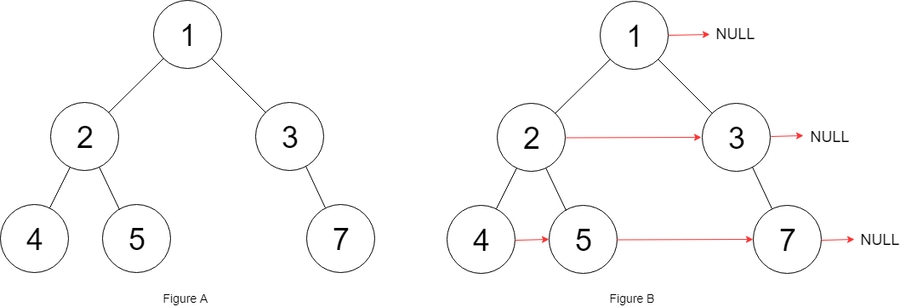
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 6000].

• -100 <= Node.val <= 100

Follow-up:

• You may only use constant extra space.

• The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Solution

Approach #0

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil {
        return nil
    }
    var pre *Node
    queue := []*Node{root}
    for len(queue) > 0 {
        size := len(queue)
        pre = nil
        for i := 0; i < size; i++ {
            cell := queue[i]
            if pre != nil {
                pre.Next = cell
            }
            pre = cell
            if cell.Left != nil {
                queue = append(queue, cell.Left)
            }
            if cell.Right != nil {
                queue = append(queue, cell.Right)
            }
        }
        queue = queue[size:]
    }
    return root
}

Approach #1

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    start := root
    for start != nil {
        var nextStart, pre *Node
        handle := func(cur *Node) {
            if cur == nil {
                return
            }
            if nextStart == nil {
                nextStart = cur
            }
            if pre != nil {
                pre.Next = cur
            }
            pre = cur
        }
        for p := start; p != nil; p = p.Next {
            handle(p.Left)
            handle(p.Right)
        }
        start = nextStart
    }
    return root
}

572. Subtree of Another Tree

Description

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

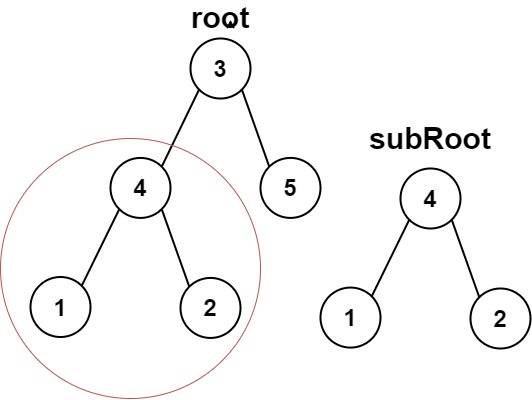
Example 2:

Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

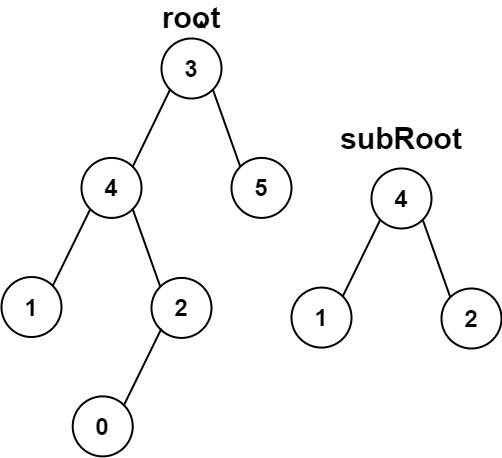
Constraints:

• The number of nodes in the root tree is in the range [1, 2000].

• The number of nodes in the subRoot tree is in the range [1, 1000].

• -10^4 <= root.val <= 10^4

• -10^4 <= subRoot.val <= 10^4

Solution

Approach #0

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSubtree(root *TreeNode, subRoot *TreeNode) bool {
    if root == nil {
        return false
    }
    return cmp(root, subRoot) || isSubtree(root.Left, subRoot) || isSubtree(root.Right, subRoot)

}

func cmp(root *TreeNode, subRoot *TreeNode) bool {
    if root == nil && subRoot == nil {
        return true
    }
    if root == nil || subRoot == nil {
        return false
    }
    if root.Val == subRoot.Val {
        return cmp(root.Left, subRoot.Left) && cmp(root.Right, subRoot.Right)
    }
    return false
}