2022-06-04

1091. Shortest Path in Binary Matrix

Description

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

• All the visited cells of the path are 0.

• All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

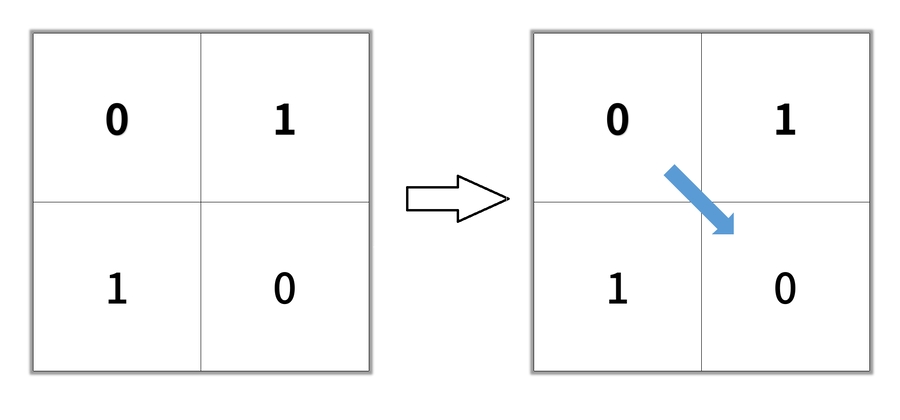
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

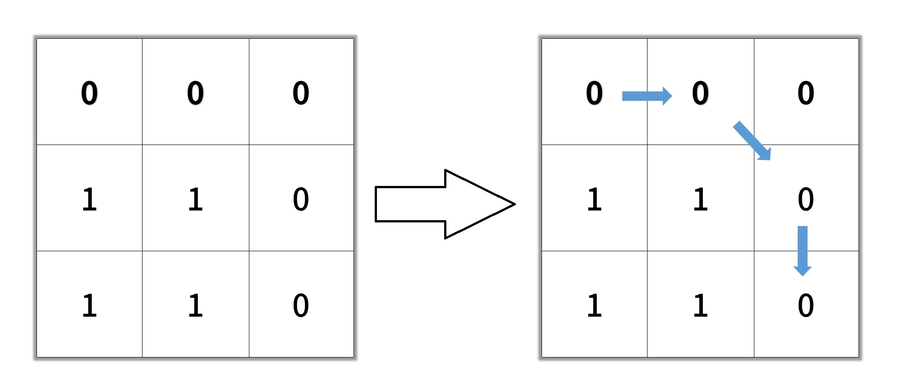
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

• n == grid.length

• n == grid[i].length

• 1 <= n <= 100

• grid[i][j] is 0 or 1

Solution

Approach #0

var (
    dx = []int{-1, -1, -1, 0, 1, 1, 1, 0}
    dy = []int{-1, 0, 1, 1, 1, 0, -1, -1}
)

func shortestPathBinaryMatrix(grid [][]int) int {
    if grid[0][0] == 1 {
        return -1
    }
    m, n := len(grid), len(grid[0])
    if m == 1 && n == 1 && grid[0][0] == 0 {
        return 1
    }
    queue := [][]int{{0, 0}}
    depth := 1
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            x, y := queue[i][0], queue[i][1]
            for j := 0; j < 8; j++ {
                xx, yy := x+dx[j], y+dy[j]
                if xx >= 0 && xx < m && yy >= 0 && yy < n && grid[xx][yy] == 0 {
                    if xx == m-1 && yy == n-1 {
                        return depth + 1
                    }
                    grid[xx][yy] = 1
                    queue = append(queue, []int{xx, yy})
                }
            }
        }
        queue = queue[size:]
        depth += 1
    }
    return -1
}

130. Surrounded Regions

Description

Given an m x n matrix board containing 'X' and 'O', capture all regions that are 4-directionally surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example 1:

Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

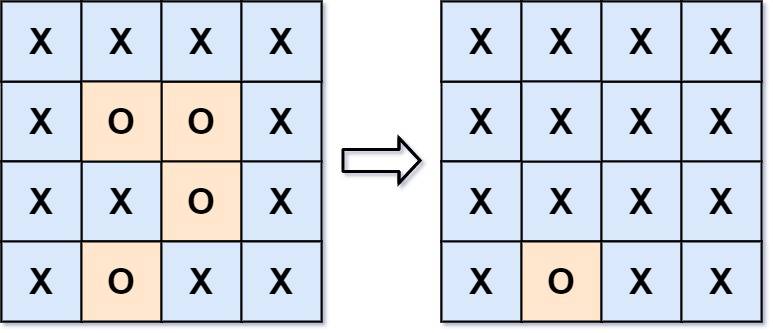
Example 2:

Input: board = [["X"]]
Output: [["X"]] 

Constraints:

• m == board.length

• n == board[i].length

• 1 <= m, n <= 200

• board[i][j] is 'X' or 'O'.

Solution

Approach #0: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func solve(board [][]byte) {
    m, n := len(board), len(board[0])
    var queue [][]int
    for i := 0; i < n; i++ {
        if board[0][i] != 'X' {
            board[0][i] = '-'
            queue = append(queue, []int{0, i})
        }
        if board[m-1][i] != 'X' {
            board[m-1][i] = '-'
            queue = append(queue, []int{m - 1, i})
        }
    }
    for i := 1; i < m-1; i++ {
        if board[i][0] != 'X' {
            board[i][0] = '-'
            queue = append(queue, []int{i, 0})
        }
        if board[i][n-1] != 'X' {
            board[i][n-1] = '-'
            queue = append(queue, []int{i, n - 1})
        }
    }
    for len(queue) > 0 {
        x, y := queue[0][0], queue[0][1]
        queue = queue[1:]
        for i := 0; i < 4; i++ {
            xx, yy := x+dx[i], y+dy[i]
            if xx >= 0 && xx < m && yy >= 0 && yy < n && board[xx][yy] == 'O' {
                queue = append(queue, []int{xx, yy})
                board[xx][yy] = '-'
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if board[i][j] == '-' {
                board[i][j] = 'O'
            } else {
                board[i][j] = 'X'
            }
        }
    }
}

Approach #1: DFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func solve(board [][]byte) {
    m, n := len(board), len(board[0])
    var dfs func(board [][]byte, x, y int)
    dfs = func(board [][]byte, x, y int) {
        if x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O' {
            return
        }
        board[x][y] = '-'
        for i := 0; i < 4; i++ {
            xx, yy := x+dx[i], y+dy[i]
            dfs(board, xx, yy)
        }
    }
    for i := 0; i < n; i++ {
        dfs(board, 0, i)
        dfs(board, m-1, i)
    }
    for i := 1; i < m-1; i++ {
        dfs(board, i, 0)
        dfs(board, i, n-1)
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if board[i][j] == '-' {
                board[i][j] = 'O'
            } else {
                board[i][j] = 'X'
            }
        }
    }
}

797. All Paths From Source to Target

Description

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

Example 1:

Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

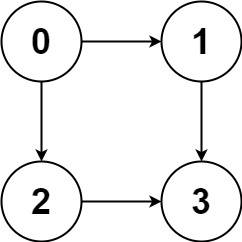
Example 2:

Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

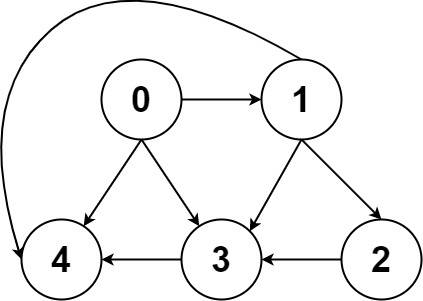
Constraints:

• n == graph.length

• 2 <= n <= 15

• 0 <= graph[i][j] < n

• graph[i][j] != i (i.e., there will be no self-loops).

• All the elements of graph[i] are unique.

• The input graph is guaranteed to be a DAG.

Solution

Approach #0: DFS

func allPathsSourceTarget(graph [][]int) (ans [][]int) {
    n:=len(graph)
    
    var dfs func(index int, cur []int)
    dfs = func(index int, cur []int) {
        cur=append(cur, index)
        for _,i:=range graph[index] {
            if i+1==n {
                c:=make([]int,len(cur))
                copy(c,cur)
                c=append(c,i)
                ans=append(ans,c)
                continue
            }
            dfs(i,cur)
        }
    }
    var cur []int
    dfs(0,cur)
    return
}

Approach #1: BFS

func allPathsSourceTarget(graph [][]int) (ans [][]int) {
    n := len(graph)
    queue := [][]int{{0}}
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            l := queue[i]
            last := len(l) - 1
            if l[last] == n-1 {
                a := make([]int, len(l))
                copy(a, l)
                ans = append(ans, a)
                continue
            }
            for _, e := range graph[l[last]] {
                a := make([]int, len(l))
                copy(a, l)
                a = append(a, e)
                queue = append(queue, a)
            }
        }
        queue = queue[size:]
    }
    return
}