2022-05-23

542. 01 Matrix

Description

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

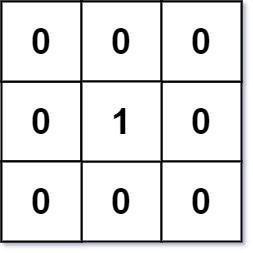
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
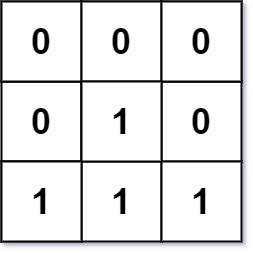
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 10^4

• 1 <= m * n <= 10^4

• mat[i][j] is either 0 or 1.

• There is at least one 0 in mat.

Solution

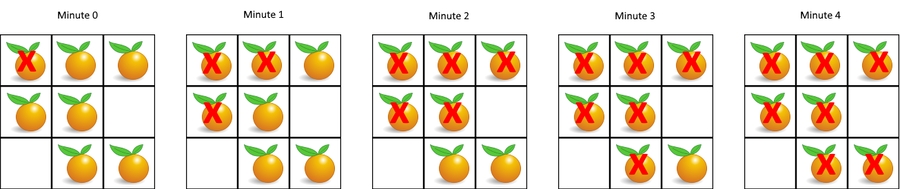
Approach #0: BFS (Time Limit Exceeded) ❌

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func updateMatrix(mat [][]int) [][]int {
    if len(mat) == 0 {
        return mat
    }
    m, n := len(mat), len(mat[0])

    res := make([][]int, m)
    for i := 0; i < m; i++ {
        res[i] = make([]int, n)
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            queue := [][]int{{i, j}}
            depth := -1
            t := make([][]int, m)
            for i := 0; i < m; i++ {
                t[i] = make([]int, n)
            }
            for len(queue) > 0 {
                size := len(queue)
                for k := 0; k < size; k++ {
                    x, y := queue[k][0], queue[k][1]
                    t[x][y] = 1
                    if mat[x][y] == 0 {
                        queue = queue[:0]
                        break
                    } else {
                        for p := 0; p < 4; p++ {
                            xx, yy := x+dx[p], y+dy[p]
                            if xx >= 0 && xx < m && yy >= 0 && yy < n && t[xx][yy] != 1 {
                                queue = append(queue, []int{xx, yy})
                            }
                        }
                    }
                }
                depth++
                if len(queue) > 0 {
                    queue = queue[size:]
                }

            }
            res[i][j] = depth
        }
    }
    return res
}

Approach #1: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func updateMatrix(mat [][]int) [][]int {
    if len(mat) == 0 {
        return mat
    }
    m, n := len(mat), len(mat[0])

    res := make([][]int, m)
    checked := make([][]int, m)
    for i := 0; i < m; i++ {
        res[i] = make([]int, n)
        checked[i] = make([]int, n)
    }

    var queue [][]int
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if mat[i][j] == 0 {
                queue = append(queue, []int{i, j})
                checked[i][j] = 1
            }
        }
    }

    depth := 0
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            x, y := queue[i][0], queue[i][1]
            res[x][y] = depth
            for p := 0; p < 4; p++ {
                xx, yy := x+dx[p], y+dy[p]
                if xx >= 0 && xx < m && yy >= 0 && yy < n && checked[xx][yy] != 1 {
                    checked[xx][yy] = 1
                    queue = append(queue, []int{xx, yy})
                }
            }
        }
        depth++
        queue = queue[size:]
    }

    return res
}

994. Rotting Oranges

Description

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,

• 1 representing a fresh orange, or

• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 10

• grid[i][j] is 0, 1, or 2.

Solution

Approach #0: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func orangesRotting(grid [][]int) int {
    if len(grid) == 0 {
        return 0
    }
    m, n := len(grid), len(grid[0])
    all1 := 0
    var queue [][]int
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == 1 {
                all1++
            }
            if grid[i][j] == 2 {
                queue = append(queue, []int{i, j})
            }
        }
    }
    if len(queue) == 0 && all1 == 0 {
        return 0
    }

    depth := -1
    count1 := -len(queue)
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            x, y := queue[i][0], queue[i][1]
            count1++
            for j := 0; j < 4; j++ {
                xx, yy := x+dx[j], y+dy[j]
                if xx >= 0 && xx < m && yy >= 0 && yy < n && grid[xx][yy] == 1 {
                    grid[xx][yy] = 2
                    queue = append(queue, []int{xx, yy})
                }
            }

        }
        fmt.Println(all1, count1)
        depth++
        queue = queue[size:]
    }
    if all1 > count1 {
        return -1
    }
    return depth
}