2022-06-02

200. Number of Islands

Description

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Example 2:

Input: grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
Output: 3

Constraints:

  • m == grid.length

  • n == grid[i].length

  • 1 <= m, n <= 300

  • grid[i][j] is '0' or '1'.

Solution

Approach #0: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func numIslands(grid [][]byte) (ans int) {
    if len(grid) == 0 {
        return 0
    }
    m, n := len(grid), len(grid[0])
    var queue [][]int
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == '0' {
                continue
            }
            ans++
            queue = append(queue, []int{i, j})
            for len(queue) > 0 {
                x, y := queue[0][0], queue[0][1]
                queue = queue[1:]
                if grid[x][y] == '0' {
                    continue
                }
                grid[x][y] = '0'
                for k := 0; k < 4; k++ {
                    xx, yy := x+dx[k], y+dy[k]
                    if xx >= 0 && xx < m && yy >= 0 && yy < n && grid[xx][yy] > '0' {
                        queue = append(queue, []int{xx, yy})
                    }
                }
            }
        }
    }
    return ans
}

Approach #1: DFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func numIslands(grid [][]byte) (ans int) {
    if len(grid) == 0 {
        return 0
    }
    m, n := len(grid), len(grid[0])
    var dfs func(x, y int)
    dfs = func(x, y int) {
        if grid[x][y] == '0' {
            return
        }
        grid[x][y] = '0'
        for i := 0; i < 4; i++ {
            xx, yy := x+dx[i], y+dy[i]
            if xx >= 0 && xx < m && yy >= 0 && yy < n && grid[xx][yy] > '0' {
                dfs(xx, yy)
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == '0' {
                continue
            }
            ans++
            dfs(i, j)
        }
    }
    return ans
}

547. Number of Provinces

Description

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

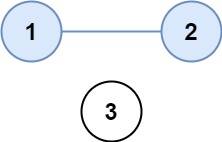
Example 2:

Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

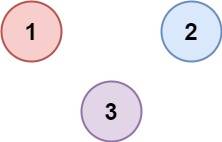
Constraints:

  • 1 <= n <= 200

  • n == isConnected.length

  • n == isConnected[i].length

  • isConnected[i][j] is 1 or 0.

  • isConnected[i][i] == 1

  • isConnected[i][j] == isConnected[j][i]

Solution

Approach #0

func findCircleNum(isConnected [][]int) (ans int) {
    if len(isConnected) == 0 {
        return 0
    }
    m := len(isConnected)
    var dfs func(x, y int)
    dfs = func(x, y int) {
        for i := 0; i < m; i++ {
            if isConnected[y][i] == 0 {
                continue
            }
            isConnected[y][i] = 0
            if isConnected[i][y] > 0 {
                dfs(y, i)
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < m; j++ {
            if isConnected[i][j] == 0 {
                continue
            }
            ans++
            if isConnected[j][i] > 0 {
                dfs(i, j)
            }
        }
    }
    return ans
}

Approach #1

func findCircleNum(isConnected [][]int) (ans int) {
    if len(isConnected) == 0 {
        return 0
    }
    m := len(isConnected)
    vis := make([]bool, m)
    var queue []int
    for i, ok := range vis {
        if !ok {
            ans++
            queue = append(queue, i)
            for len(queue) > 0 {
                j := queue[0]
                vis[j] = true
                queue = queue[1:]
                for k := 0; k < m; k++ {
                    if isConnected[j][k] == 1 && !vis[k] {
                        queue = append(queue, k)
                    }
                }
            }
        }
    }
    return ans
}

450. Delete Node in a BST

Description

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

  1. Search for a node to remove.

  2. If the node is found, delete the node.

Example 1:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

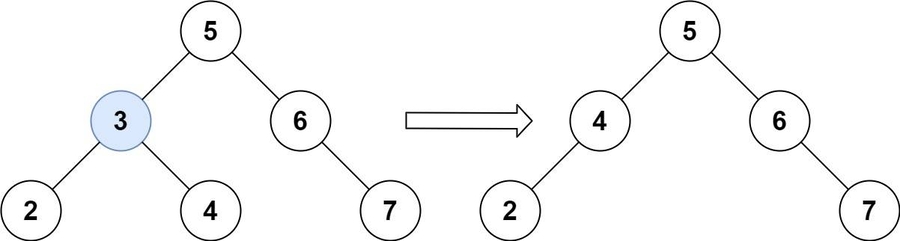
Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 10^4].

  • -10^5 <= Node.val <= 10^5

  • Each node has a unique value.

  • root is a valid binary search tree.

  • -10^5 <= key <= 10^5

Follow up: Could you solve it with time complexity O(height of tree)?

Solution

Approach #0

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func deleteNode(root *TreeNode, key int) *TreeNode {
    var pre *TreeNode
    cur := root
    for cur != nil {
        if cur.Val == key {
            if cur.Left == nil {
                if cur == root {
                    return root.Right
                }
                if pre.Val > cur.Val {
                    pre.Left = cur.Right
                } else {
                    pre.Right = cur.Right
                }
                return root
            }
            if cur.Right == nil {
                if cur == root {
                    return root.Left
                }
                if pre.Val > cur.Val {
                    pre.Left = cur.Left
                } else {
                    pre.Right = cur.Left
                }
                return root
            }
            target := cur
            pre = cur
            cur = cur.Right
            for cur.Left != nil {
                pre = cur
                cur = cur.Left
            }
            if pre.Val > cur.Val {
                pre.Left = cur.Right
            } else {
                pre.Right = cur.Right
            }
            target.Val = cur.Val
            return root
        }
        pre = cur
        if cur.Val > key {
            cur = cur.Left
        } else {
            cur = cur.Right
        }
    }
    return root
}

Approach #1: Recursive

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func deleteNode(root *TreeNode, key int) *TreeNode {
    switch {
    case root == nil:
        return nil
    case root.Val > key:
        root.Left = deleteNode(root.Left, key)
    case root.Val < key:
        root.Right = deleteNode(root.Right, key)
    case root.Left == nil:
        return root.Right
    case root.Right == nil:
        return root.Left
    default:
        cur := root.Right
        for cur.Left != nil {
            cur = cur.Left
        }
        cur.Right = deleteNode(root.Right, cur.Val)
        cur.Left = root.Left
        return cur
    }
    return root
}

Last updated