2022-05-30
Description
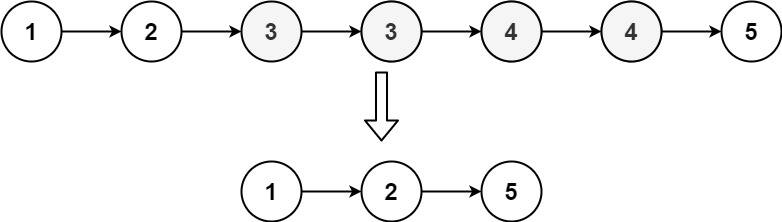
Input: head = [1,2,3,3,4,4,5]
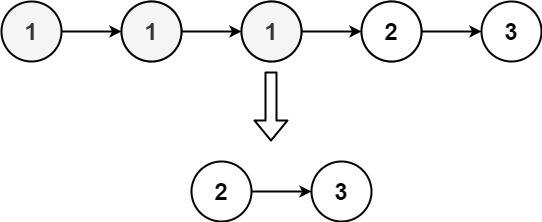
Output: [1,2,5]Input: head = [1,1,1,2,3]
Output: [2,3]Solution
Approach #0
Approach #1
Description
Solution
Approach #0
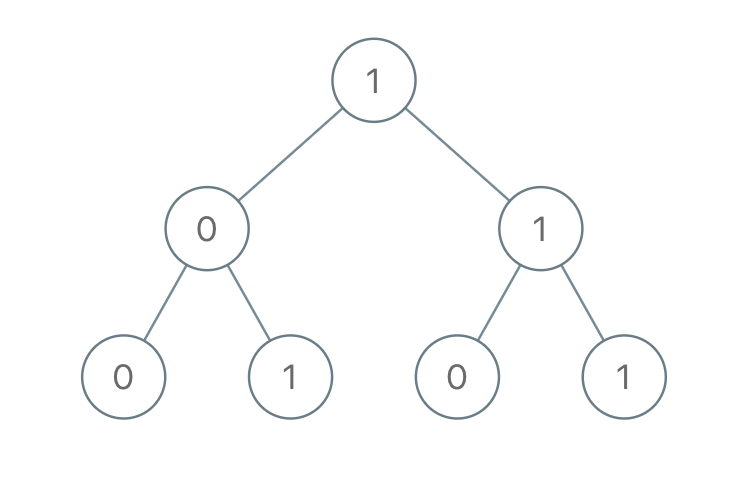
Description
Solution
Approach #0
Approach #1
Last updated