2022-06-09

45. Jump Game II

Description

Given an array of non-negative integers nums, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Your goal is to reach the last index in the minimum number of jumps.

You can assume that you can always reach the last index.

Example 1:

Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

Input: nums = [2,3,0,1,4]
Output: 2

Constraints:

• 1 <= nums.length <= 10^4

• 0 <= nums[i] <= 1000

Solution

Approach #0

func jump(nums []int) (ans int) {
    p, maxPos := 0, 0
    for i := 0; i < len(nums)-1; i++ {
        maxPos = max(maxPos, i+nums[i])
        if p == i {
            p = maxPos
            ans++
        }
    }
    return
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}45

62. Unique Paths

Description

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

Input: m = 3, n = 7
Output: 28

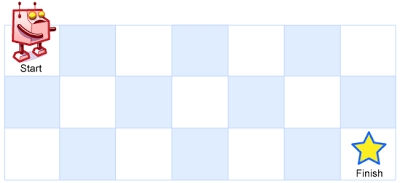
Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Constraints:

• 1 <= m, n <= 100

Solution

Approach #0

func uniquePaths(m int, n int) int {
    dp := make([][]int, m)
    for i := range dp {
        dp[i] = make([]int, n)
        dp[i][0] = 1
    }
    for i := 1; i < n; i++ {
        dp[0][i] = 1
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
        }
    }
    return dp[m-1][n-1]
}