2022-05-21

733. Flood Fill

Description

An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and newColor. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with newColor.

Return the modified image after performing the flood fill.

Example 1:

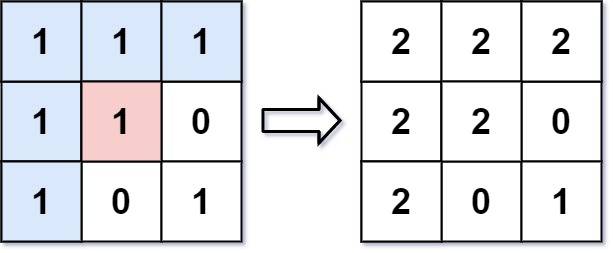
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, newColor = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation: From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not 4-directionally connected to the starting pixel.

Example 2:

Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
Output: [[2,2,2],[2,2,2]]

Constraints:

m == image.length
n == image[i].length
1 <= m, n <= 50
0 <= image[i][j], newColor < 2^16
0 <= sr < m
0 <= sc < n

Solution

Approach #0: DFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    if image[sr][sc] != newColor {
        originColor := image[sr][sc]
        dfs(image, sr, sc, originColor, newColor)
    }
    return image
}

func dfs(image [][]int, sr int, sc int, originColor, newColor int) {
    if image[sr][sc] == originColor {
        image[sr][sc] = newColor
        for i := 0; i < 4; i++ {
            newSr, newSc := sr+dx[i], sc+dy[i]
            if newSr >= 0 && newSr < len(image) && newSc >= 0 && newSc < len(image[0]) {
                dfs(image, newSr, newSc, originColor, newColor)
            }
        }
    }
}

Approach #1: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    if image[sr][sc] == newColor {
        return image
    }
    originColor := image[sr][sc]
    image[sr][sc] = newColor
    queue := [][]int{[]int{sr, sc}}
    for i := 0; i < len(queue); i++ {
        for j := 0; j < 4; j++ {
            x, y := queue[i][0]+dx[j], queue[i][1]+dy[j]
            if x >= 0 && x < len(image) && y >= 0 && y < len(image[0]) && image[x][y] == originColor {
                image[x][y] = newColor
                queue = append(queue, []int{x, y})

            }
        }
    }
    return image
}

695. Max Area of Island

Description

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] is either 0 or 1.

Solution

Approach #0: BFS

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func maxAreaOfIsland(grid [][]int) int {
    if len(grid) == 0 {
        return 0
    }
    m, n := len(grid), len(grid[0])

    res := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == 0 {
                continue
            }
            grid[i][j] = 0
            queue := [][]int{{i, j}}
            area := 1
            for ii := 0; ii < len(queue); ii++ {
                cell := queue[ii]
                for jj := 0; jj < 4; jj++ {
                    x, y := cell[0]+dx[jj], cell[1]+dy[jj]
                    if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > 0 {
                        grid[x][y] = 0
                        area++
                        queue = append(queue, []int{x, y})
                    }
                }
            }
            res = max(res, area)
        }
    }
    return res
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

Approach #1: DFS (Recursive)

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func maxAreaOfIsland(grid [][]int) int {
    if len(grid) == 0 {
        return 0
    }

    res := 0
    for i := 0; i < len(grid); i++ {
        for j := 0; j < len(grid[0]); j++ {
            if grid[i][j] == 0 {
                continue
            }
            area := dfs(grid, i, j)
            res = max(res, area)
        }
    }
    return res
}

func dfs(grid [][]int, x, y int) int {
    grid[x][y] = 0
    res := 1
    for i := 0; i < 4; i++ {
        xx, yy := x+dx[i], y+dy[i]
        if xx >= 0 && xx < len(grid) && yy >= 0 && yy < len(grid[0]) && grid[xx][yy] > 0 {
            res = res + dfs(grid, xx, yy)
        }
    }
    return res
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

Approach #2: DFS + Stack (Iterative)

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func maxAreaOfIsland(grid [][]int) int {
    if len(grid) == 0 {
        return 0
    }

    res := 0
    for i := 0; i < len(grid); i++ {
        for j := 0; j < len(grid[0]); j++ {
            s := [][]int{{i, j}}
            area := 0
            for len(s) > 0 {
                cell := s[len(s)-1]
                s = s[:len(s)-1]
                x, y := cell[0], cell[1]
                if x < 0 || x >= len(grid) || y < 0 || y >= len(grid[0]) || grid[x][y] == 0 {
                    continue
                }
                grid[x][y] = 0
                area++
                for i := 0; i < 4; i++ {
                    xx, yy := x+dx[i], y+dy[i]
                    s = append(s, []int{xx, yy})
                }

            }
            res = max(res, area)
        }
    }
    return res
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

Last updated 1 year ago