2022-05-24

21. Merge Two Sorted Lists

Description

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists in a one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

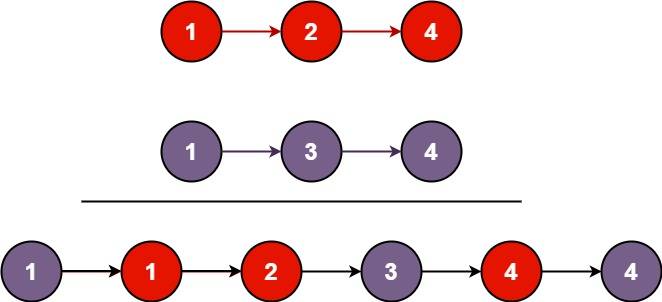
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

Constraints:

  • The number of nodes in both lists is in the range [0, 50].

  • -100 <= Node.val <= 100

  • Both list1 and list2 are sorted in non-decreasing order.

Solution

Approach #0

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
    root := &ListNode{}
    cur := root
    for list1 != nil && list2 != nil {
        if list1.Val < list2.Val {
            cur.Next = list1
            cur = cur.Next
            list1 = list1.Next
        } else {
            cur.Next = list2
            cur = cur.Next
            list2 = list2.Next
        }
    }
    if list1 != nil {
        cur.Next = list1
    }
    if list2 != nil {
        cur.Next = list2
    }
    return root.Next
}

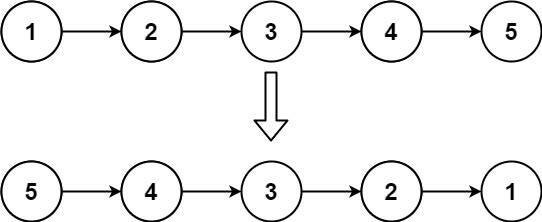
Approach #1: Recursive

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
    if list1 == nil {
        return list2
    }
    if list2 == nil {
        return list1
    }
    if list1.Val < list2.Val {
        list1.Next = mergeTwoLists(list1.Next, list2)
        return list1
    } else {
        list2.Next = mergeTwoLists(list1, list2.Next)
        return list2
    }
}

206. Reverse Linked List

Description

Given the head of a singly linked list, reverse the list, and return the reversed list.

Example 1:

Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]

Example 2:

Input: head = [1,2]
Output: [2,1]

Example 3:

Input: head = []
Output: []

Constraints:

  • The number of nodes in the list is the range [0, 5000].

  • -5000 <= Node.val <= 5000

Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?

Solution

Approach #0: Iterative

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func reverseList(head *ListNode) *ListNode {
    if head == nil {
        return nil
    }
    cur := head
    var prev *ListNode
    for cur.Next != nil {
        next := cur.Next
        cur.Next = prev
        prev = cur
        cur = next
    }
    cur.Next = prev
    return cur
}

Approach #1: Recursive

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func reverseList(head *ListNode) *ListNode {
    if head == nil {
        return head
    }
    return reverse(head, nil)
}

func reverse(cur, prev *ListNode) *ListNode {
    next := cur.Next
    cur.Next = prev
    if next == nil {
        return cur
    } else {
        return reverse(next, cur)
    }
}

1480. Running Sum of 1d Array

Description

Given an array nums. We define a running sum of an array as runningSum[i] = sum(nums[0]…nums[i]).

Return the running sum of nums.

Example 1:

Input: nums = [1,2,3,4]
Output: [1,3,6,10]
Explanation: Running sum is obtained as follows: [1, 1+2, 1+2+3, 1+2+3+4].

Example 2:

Input: nums = [1,1,1,1,1]
Output: [1,2,3,4,5]
Explanation: Running sum is obtained as follows: [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1].

Example 3:

Input: nums = [3,1,2,10,1]
Output: [3,4,6,16,17]

Constraints:

  • 1 <= nums.length <= 1000

  • -10^6 <= nums[i] <= 10^6

Solution

Approach #0

func runningSum(nums []int) []int {
    for i := 1; i < len(nums); i++ {
        nums[i] = nums[i] + nums[i-1]
    }
    return nums
}

383. Ransom Note

Description

Given two strings ransomNote and magazine, return true if ransomNote can be constructed from magazine and false otherwise.

Each letter in magazine can only be used once in ransomNote.

Example 1:

Input: ransomNote = "a", magazine = "b"
Output: false

Example 2:

Input: ransomNote = "aa", magazine = "ab"
Output: false

Example 3:

Input: ransomNote = "aa", magazine = "aab"
Output: true

Constraints:

  • 1 <= ransomNote.length, magazine.length <= 10^5

  • ransomNote and magazine consist of lowercase English letters.

Solution

Approach #0

func canConstruct(ransomNote string, magazine string) bool {
    var m [26]int
    for i := 0; i < len(magazine); i++ {
        m[magazine[i]-'a']++
    }
    for i := 0; i < len(ransomNote); i++ {
        m[ransomNote[i]-'a']--
        if m[ransomNote[i]-'a'] < 0 {
            return false
        }
    }
    return true
}

965. Univalued Binary Tree

Description

A binary tree is uni-valued if every node in the tree has the same value.

Given the root of a binary tree, return true if the given tree is uni-valued, or false otherwise.

Example 1:

Input: root = [1,1,1,1,1,null,1]
Output: true

Example 2:

Input: root = [2,2,2,5,2]
Output: false

Constraints:

  • The number of nodes in the tree is in the range [1, 100].

  • 0 <= Node.val < 100

Solution

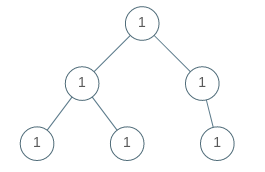
Approach #0: BFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isUnivalTree(root *TreeNode) bool {
    queue := []*TreeNode{root}
    v := root.Val
    for i := 0; i < len(queue); i++ {
        if queue[i].Val != v {
            return false
        }
        if queue[i].Left != nil {
            queue = append(queue, queue[i].Left)
        }
        if queue[i].Right != nil {
            queue = append(queue, queue[i].Right)
        }
    }
    return true
}

Approach #1: DFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isUnivalTree(root *TreeNode) bool {
    if root == nil {
        return true
    }
    if root.Left != nil && root.Val != root.Left.Val || !isUnivalTree(root.Left) {
        return false
    }
    if root.Right != nil && root.Val != root.Right.Val || !isUnivalTree(root.Right) {
        return false
    }
    return true
}

Last updated