2022-06-07

17. Letter Combinations of a Phone Number

Description

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.

A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example 1:

Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]

Example 2:

Input: digits = ""
Output: []

Example 3:

Input: digits = "2"
Output: ["a","b","c"]

Constraints:

• 0 <= digits.length <= 4

• digits[i] is a digit in the range ['2', '9'].

Solution

Approach #0

var keyboard = map[byte]string {
    '2':"abc",
    '3':"def",
    '4':"ghi",
    '5':"jkl",
    '6':"mno",
    '7':"pqrs",
    '8':"tuv",
    '9':"wxyz",
}
func letterCombinations(digits string) (ans []string) {
    n:=len(digits)
    if n==0 {
        return
    }
    var b func(cur int, str string)
    b=func(cur int, str string) {
        if cur==n {
            ans = append(ans, str)
            return
        }
        for _, ch := range keyboard[digits[cur]] {
            b(cur+1, str+string(ch))
        }
    }
    b(0,"")
    return
}

22. Generate Parentheses

Description

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Example 2:

Input: n = 1
Output: ["()"]

Constraints:

• 1 <= n <= 8

Solution

Approach #0

func generateParenthesis(n int) (ans []string) {
    var tmp []byte
    var b func(left, right int)
    b = func(left, right int) {
        if len(tmp) == n*2 {
            ans = append(ans, string(tmp))
            return
        }
        if left < n {
            tmp = append(tmp, '(')
            b(left+1, right)
            tmp = tmp[:len(tmp)-1]
        }
        if right < left {
            tmp = append(tmp, ')')
            b(left, right+1)
            tmp = tmp[:len(tmp)-1]
        }
    }
    b(0, 0)
    return
}

79. Word Search

Description

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

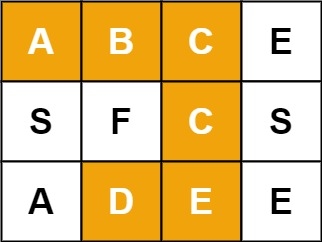
Example 2:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

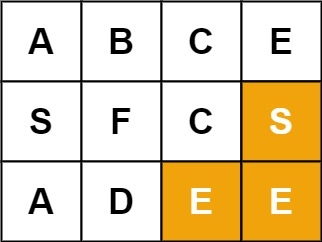
Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m == board.length

• n = board[i].length

• 1 <= m, n <= 6

• 1 <= word.length <= 15

• board and word consists of only lowercase and uppercase English letters.

Follow up: Could you use search pruning to make your solution faster with a larger board?

Solution

Approach #0

var (
    dx = []int{0, 1, 0, -1}
    dy = []int{1, 0, -1, 0}
)

func exist(board [][]byte, word string) bool {
    m, n := len(board), len(board[0])
    vis := make([][]bool, m)
    for i := range vis {
        vis[i] = make([]bool, n)
    }
    var b func(x, y, index int) bool
    b = func(x, y, index int) bool {
        if board[x][y] != word[index] {
            return false
        }
        if index == len(word)-1 {
            return true
        }
        vis[x][y] = true
        defer func() { vis[x][y] = false }()
        for i := 0; i < 4; i++ {
            xx, yy := x+dx[i], y+dy[i]
            if xx >= 0 && xx < m && yy >= 0 && yy < n && !vis[xx][yy] {
                if b(xx, yy, index+1) {
                    return true
                }
            }
        }
        return false
    }
    for i, row := range board {
        for j := range row {
            if b(i, j, 0) {
                return true
            }
        }
    }
    return false
}