2022-05-22

617. Merge Two Binary Trees

Description

You are given two binary trees root1 and root2.

Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.

Return the merged tree.

Note: The merging process must start from the root nodes of both trees.

Example 1:

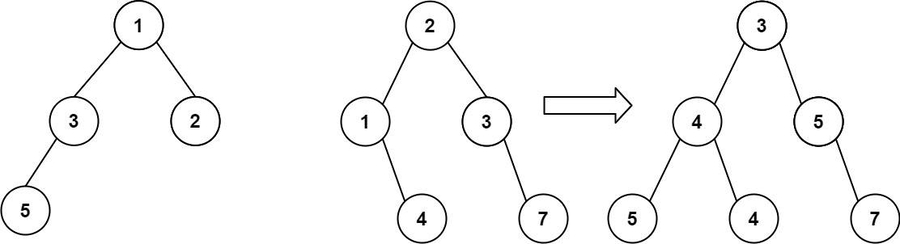
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]

Example 2:

Input: root1 = [1], root2 = [1,2]
Output: [2,2]

Constraints:

• The number of nodes in both trees is in the range [0, 2000].

• -10^4 <= Node.val <= 10^4

Solution

Approach #0: DFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
    if root1 == nil {
        return root2
    }
    if root2 == nil {
        return root1
    }
    root1.Val = root1.Val + root2.Val
    root1.Left = mergeTrees(root1.Left, root2.Left)
    root1.Right = mergeTrees(root1.Right, root2.Right)
    return root1
}

Approach #1: BFS

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
    if root1 == nil {
        return root2
    }
    if root2 == nil {
        return root1
    }
    queue := [][]*TreeNode{{root1, root2}}
    for i := 0; i < len(queue); i++ {
        a, b := queue[i][0], queue[i][1]
        if b != nil {
            a.Val = a.Val + b.Val
            if a.Left != nil && b.Left != nil {
                queue = append(queue, []*TreeNode{a.Left, b.Left})
            } else {
                if a.Left != nil {
                    queue = append(queue, []*TreeNode{a.Left, nil})
                }
                if b.Left != nil {
                    a.Left = &TreeNode{Val: 0}
                    queue = append(queue, []*TreeNode{a.Left, b.Left})
                }
            }
            if a.Right != nil && b.Right != nil {
                queue = append(queue, []*TreeNode{a.Right, b.Right})
            } else {
                if a.Right != nil {
                    queue = append(queue, []*TreeNode{a.Right, nil})
                }
                if b.Right != nil {
                    a.Right = &TreeNode{Val: 0}
                    queue = append(queue, []*TreeNode{a.Right, b.Right})
                }
            }
        } else {
            if a.Left != nil {
                queue = append(queue, []*TreeNode{a.Left, nil})
            }
            if a.Right != nil {
                queue = append(queue, []*TreeNode{a.Right, nil})
            }
        }

    }
    return root1
}

116. Populating Next Right Pointers in Each Node

Description

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

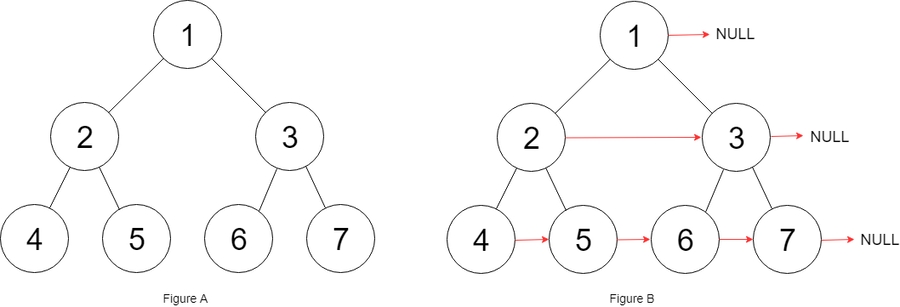
Example 2:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 2^12 - 1].

• -1000 <= Node.val <= 1000

Follow-up:

• You may only use constant extra space.

• The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Solution

Approach #0: BFS

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil {
        return root
    }
    queue := []*Node{root}
    for len(queue) > 0 {
        size := len(queue)
        for i := 0; i < size; i++ {
            if i+1 < size {
                queue[i].Next = queue[i+1]
            }
            if queue[i].Left != nil {
                queue = append(queue, queue[i].Left, queue[i].Right)
            }

        }
        queue = queue[size:]
    }
    return root
}

Approach #1: DFS (Iterative)

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    for l := root; l.Left != nil; l = l.Left {
        for node := l; node != nil; node = node.Next {
            node.Left.Next = node.Right
            if node.Next != nil {
                node.Right.Next = node.Next.Left
            }
        }
    }
    return root
}

Approach #2: DFS (Recursive)

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil {
        return root
    }
    dfs(root, nil)
    return root
}

func dfs(left, next *Node) {
    if left == nil {
        return
    }
    left.Next = next
    dfs(left.Left, left.Right)
    if left.Next == nil {
        dfs(left.Right, nil)
    } else {
        dfs(left.Right, left.Next.Left)
    }
}